Nella vecchia banconota dei 10 marchi tedeschi troneggia il volto serio di Gauss, a mio avviso il matematico più grande del mondo, in assoluto, perché già alla fin del ‘700 aveva tracciato le basi dell’attuale analisi matematica.
In realtà non si sa bene se ciò di cui parleremo oggi, cioè il <metodo dei minimi quadrati> si debba a Laplace o a Gauss: di certo Laplace fece ampie e rigorose dimostrazioni mentre Gauss lo utilizzò per predire puntualmente la posizione di Cerere nella meccanica celeste.
Gauss o Laplace, non importa, vediamo come da qui si debba partire per arrivare all’ LRI <Linear Regression Indicator> in modo da dare una svolta significativa ai concetti elementari delle Medie Mobili di cui abbiamo parlato e che abbiamo già definito ‘fare acqua’ in più parti.
Anziché partire dai dati della Borsa, tanto per semplificare, supponiamo di aver raccolto alcuni dati di un’osservazione sperimentale qualsiasi. Vediamo:

In questo esempio, la X potrebbe essere il Tempo e la Y la velocità di una biglia lanciata su un piano ma quel che più conta è comprendere, per esempio, che nel caso n° 4 ho X = 2 e Y = 5.
Quello che realmente mi piacerebbe sapere è che cosa, secondo la statistica, sarebbe successo alla Y (la velocità della biglia) se l’avessi fotografata a un istante ‘intermedio’ <per esempio con X = 2,5>. Quale sarebbe stata la sua velocità?
Ma è ancor di più ciò che vorrei conoscere: cioè estrapolare le osservazioni di cui dispongo per trovare un dato sconosciuto: cioè cosa succederebbe in futuro, per esempio, in un ipotetico caso n°9 <oltre, cioè, il mio campo di osservazione>.
Come dice la parola stessa, il primo caso si definisce di ‘interpolazione’, il secondo caso è l’ ‘estrapolazione’.
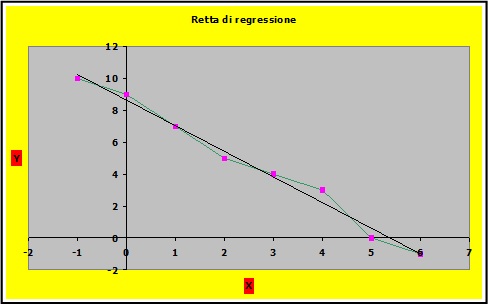
Se ora inseriamo nel grafico a due dimensioni che vedete i dati della nostra osservazione possiamo notare:
- I pallini viola corrispondono alle osservazioni
- Una linea spezzata in verde unisce i punti delle osservazioni
- Finalmente, e vedremo presto come realizzarla, in nero abbiamo la cosiddetta ‘interpolante’ quella cioè che meglio si adatta a passare attraverso la ‘nuvola’ dei pallini viola
Poiché l’interpolante del nostro esperimento è una linea retta, ciò di cui stiamo parlando è la regressione lineare.
Nota:
Non sempre l’interpolante è una retta, in altri casi può essere una conica, come per esempio una parabola o un’iperbole.
Riepilogo:
Il nostro grafico, detto a ‘dispersione’, rappresenta i punti di un esperimento di osservazioni. I punti sono collegati in verde da una spezzata, mentre l’interpolante è una retta, detta regressione lineare.
Ecco ora la domanda: esiste un’equazione che rappresenti al meglio l’interpolante lineare?
La risposta è ‘sì’ e il metodo di calcolo è quello di Gauss – Laplace, conosciuto come metodo dei minimi quadrati.
Pur evitando la dimostrazione matematica, proviamo a evidenziare il ragionamento di Gauss. Per farlo dobbiamo subito dire che la linea di regressione ha una propria equazione corrispondente. L’equazione di una retta è sempre la stessa: Y = AX +B
Come al solito parto dalla fine e vi dico subito (ma lo scopriremo insieme) che l’equazione del nostro esperimento è: y = -1,6071 X + 8,6428
Cosa significa tutto ciò?
Facile! Se prendo una coppia qualsiasi, per esempio il caso n°4, dovrò usare x = 2 e y = 5.
Quindi, se nella equazione y = -1,6071 X + 8,6428 pongo 2 nel valore x e faccio un paio di conti, ottengo 5,4286.
Che cos’è questo numero? Ma certo, è il valore nella corrispondente interpolante!
In pratica, il valore ottenuto 5,4286 è il miglior valore ottenibile a fronte della dispersione dei punti nel grafico del nostro esperimento.
Qualcuno potrebbe osservare “ma perché non ottengo ancora 5 che era il corrispondente del valore 2 nel caso 4?”. No, non è così!
La risposta è che il valore 5 è il corrispondente esatto di una certa prova dell’esperimento ma quell’esperimento mi ha consentito di trovare la retta che meglio approssima (cioè sta in mezzo nel modo migliore) quella particolare dispersione di punti. La differenza tra 5 (il valore dell’esperimento) e 5,4286 sta proprio nella conclusione del nostro lavoro, cioè l’aver trovato l’interpolante che meglio si adatta a tutto l’insieme di punti dell’esperimento.
Gauss dimostra che il modo migliore per trovare l’equazione, consista nel ‘rendere minima’ la distanza tra i punti di dispersione e la retta di approssimazione che stiamo cercando.
Ecco la definizione di Gauss: la retta dei minimi quadrati è quella retta per cui è minima la somma dei quadrati delle distanze dei punti di dispersione.
Ma adesso basta con le formule !!! Non se ne può più L.
Riprendiamo il riepilogo e aggiungiamo un pezzo nuovo:
Riepilogo:
Il nostro grafico, detto a ‘dispersione’, rappresenta i punti di un esperimento di osservazioni. I punti sono collegati in verde da una spezzata mentre l’interpolante è una retta, detta regressione lineare.
Supponendo di conoscere preventivamente l’equazione della regressione lineare, quell’equazione consente di trovare un qualsiasi valore della “velocità della nostra biglia” in un qualsiasi esperimento, tanto ‘interpolato’ <cioè dentro all’esperimento> quanto ‘estrapolato’ <cioè fuori dall’esperimento>. Se tento l’esperimento mettendo il valore 2 (del caso 4) ottengo un valore diverso dall’esperimento (5,4286 anziché 5) poiché ora non mi riferisco più alla realtà ma alla retta statistica.
La regressione lineare si ottiene tramite il metodo dei minimi quadrati ideato da Gauss e si fonda sull’ipotesi che la somma dei quadrati delle distanze tra i punti di dispersione e la retta che si deve trovare risulti minima.
Troppa carne al fuoco, oggi, ne sono consapevole  Ci fermiamo un attimo per meditare.
Ci fermiamo un attimo per meditare.
La prossima volta spieghiamo come siamo arrivati a definire che nel caso dell’esperimento n°4 (x=2 e y=5) l’equazione esatta sia la suddetta y = -1,6071 X + 8,6428.
E vedremo come il metodo dei minimi quadrati sia l’equivalente Excel della funzione =PREVISIONE(x;y_nota;x_nota).
E siccome vogliamo capire la faccenda punto per punto, da una parte useremo l’equazione dei minimi quadrati mentre dall’altra utilizzeremo Excel … e questo è il percorso per spiegare il Linear Regression Indicator (LRI), capostipite del TSF (Time Series Forecast) … l’esatto ‘antagonista moderno’ delle Medie Mobili.
A presto, sempre qui su www.francescocaranti.net
Francesco Caranti